|
|
|
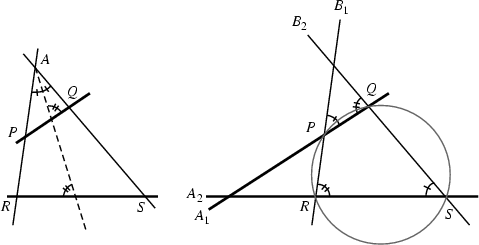
Two lines ![]() and
and ![]() are said to be antiparallel with respect to the sides of an Angle
are said to be antiparallel with respect to the sides of an Angle ![]() if they make the same
angle in the opposite senses with the Bisector of that angle. If
if they make the same
angle in the opposite senses with the Bisector of that angle. If ![]() and
and ![]() are antiparallel with
respect to
are antiparallel with
respect to ![]() and
and ![]() , then the latter are also antiparallel with respect to the former. Furthermore, if
, then the latter are also antiparallel with respect to the former. Furthermore, if ![]() and
and ![]() are
antiparallel, then the points
are
antiparallel, then the points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are Concyclic (Johnson 1929, p. 172; Honsberger 1995, pp. 87-88).
are Concyclic (Johnson 1929, p. 172; Honsberger 1995, pp. 87-88).
See also Hyperparallel, Parallel
References
Honsberger, R. ``Parallels and Antiparallels.'' §9.1 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry.
Washington, DC: Math. Assoc. Amer., pp. 87-88, 1995.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, p. 172, 1929.