|
|
|
``Analysis of Variance.'' A Statistical Test for heterogeneity of Means by analysis of group
Variances. To apply the test, assume random sampling of a variate ![]() with equal
Variances, independent errors, and a Normal Distribution. Let
with equal
Variances, independent errors, and a Normal Distribution. Let ![]() be the number of
Replicates (sets of identical observations) within each of
be the number of
Replicates (sets of identical observations) within each of ![]() Factor Levels
(treatment groups), and
Factor Levels
(treatment groups), and ![]() be the
be the ![]() th observation within Factor Level
th observation within Factor Level ![]() . Also assume that
the ANOVA is ``balanced'' by restricting
. Also assume that
the ANOVA is ``balanced'' by restricting ![]() to be the same for each Factor Level.
to be the same for each Factor Level.
Now define the sum of square terms
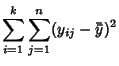 |
(1) | ||
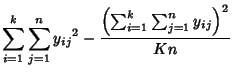 |
(2) | ||
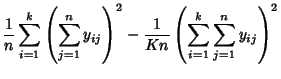 |
(3) | ||
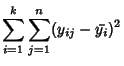 |
(4) | ||
| (5) |
| (6) |
| Category | SS | °Freedom | Mean Squared | F-Ratio |
| Treatment | SSA |
|
|
|
| Error | SSE |
|
||
| Total | SST |
|
If the P-Value is small, reject the Null Hypothesis that all Means are the same for the different groups.
See also Factor Level, Replicate, Variance
|
|
|
© 1996-9 Eric W. Weisstein