The Crossing Number for a Complete Bigraph is
where
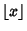 is the Floor Function. This has been shown to be true for all
is the Floor Function. This has been shown to be true for all 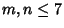 . Zarankiewicz has shown
that, in general, the Formula provides an upper bound to the actual number.
. Zarankiewicz has shown
that, in general, the Formula provides an upper bound to the actual number.
See also Complete Bigraph, Crossing Number (Graph)
© 1996-9 Eric W. Weisstein
1999-05-26