|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
A finite sequence of ![]() letters from some Alphabet is said to be an
letters from some Alphabet is said to be an ![]() -ary word. A ``square'' word consists of
two identical subwords (for example, acbacb). A squarefree word contains no square words as subwords (for
example, abcacbabcb). The only squarefree binary words are
-ary word. A ``square'' word consists of
two identical subwords (for example, acbacb). A squarefree word contains no square words as subwords (for
example, abcacbabcb). The only squarefree binary words are ![]() ,
, ![]() , ab, ba, aba, and bab.
However, there are arbitrarily long ternary squarefree words. The number of ternary squarefree words of length
, ab, ba, aba, and bab.
However, there are arbitrarily long ternary squarefree words. The number of ternary squarefree words of length ![]() is
bounded by
is
bounded by
| (1) |
| (2) |
| (3) |
A word is said to be overlapfree if it has no subwords of the form xyxyx. A squarefree word is overlapfree, and an
overlapfree word is cubefree. The number ![]() of binary overlapfree words of length
of binary overlapfree words of length ![]() satisfies
satisfies
| (4) |
| (5) |
| (6) |
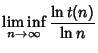 |
(7) | ||
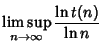 |
(8) |
See also Alphabet
References
Brandenburg, F.-J. ``Uniformly Growing
Brinkhuis, J. ``Non-Repetitive Sequences on Three Symbols.'' Quart. J. Math. Oxford Ser. 2 34, 145-149, 1983.
Cassaigne, J. ``Counting Overlap-Free Binary Words.''
STACS '93: Tenth Annual Symposium on Theoretical Aspects of Computer Science, Würzburg, Germany, February 25-27, 1993 Proceedings
(Ed. G. Goos, J. Hartmanis, A. Finkel, P. Enjalbert, K. W. Wagner). New York: Springer-Verlag, pp. 216-225, 1993.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/words/words.html
Kobayashi, Y. ``Enumeration of Irreducible Binary Words.'' Discrete Appl. Math. 20, 221-232, 1988.
Noonan, J. and Zeilberger, D. ``The Goulden-Jackson Cluster Method: Extensions, Applications, and Implementations.'' Submitted.
![]() th Power-Free Homomorphisms.'' Theor. Comput. Sci. 23, 69-82, 1983.
th Power-Free Homomorphisms.'' Theor. Comput. Sci. 23, 69-82, 1983.
|
|
|
© 1996-9 Eric W. Weisstein