|
|
|
A surface which can be interpreted as a self-intersecting Rectangle in 3-D. It is given by the parametric
equations
| (1) | |||
| (2) | |||
| (3) |
| (4) | |||
| (5) | |||
| (6) |
| (7) | |||
| (8) | |||
| (9) |
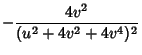 |
(10) | ||
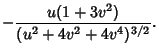 |
(11) |
References
Francis, G. K. A Topological Picturebook. New York: Springer-Verlag, pp. 8-9, 1987.
Geometry Center. ``Whitney's Umbrella.''
http://www.geom.umn.edu/zoo/features/whitney/.
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 225 and 309-310, 1993.
|
|
|
© 1996-9 Eric W. Weisstein