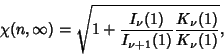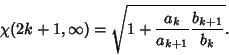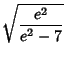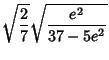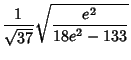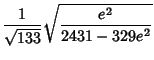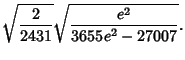N.B. A detailed on-line essay by S. Finch
was the starting point for this entry.
Let  be the
be the 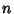 -D closed Ball of Radius
-D closed Ball of Radius 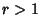 centered at the Origin. A function which is
defined on
centered at the Origin. A function which is
defined on 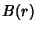 is called an extension to
is called an extension to 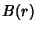 of a function
of a function 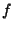 defined on
defined on 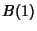 if
if
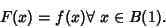 |
(1) |
Given 2 Banach Spaces of functions defined on 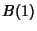 and
and 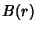 , find the extension operator from
one to the other of minimal norm. Mikhlin (1986) found the best constants
, find the extension operator from
one to the other of minimal norm. Mikhlin (1986) found the best constants 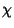 such that this condition, corresponding
to the Sobolev
such that this condition, corresponding
to the Sobolev 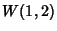 integral norm, is satisfied,
integral norm, is satisfied,
![$\sqrt{\int_{B(1)} \left[{[f(x)]^2+\sum_{j=1}^n\left({\partial f\over\partial x_j}\right)^2}\right]\,dx} $](w_772.gif)
|
|
![$ \leq \chi \sqrt{\int_{B(r)} \left[{[F(x)]^2+\sum_{j=1}^n\left({\partial F\over\partial x_j}\right)^2}\right]\,dx}\,.\quad$](w_773.gif)
|
(2) |
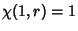 . Let
. Let
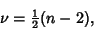 |
(3) |
then for 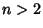 ,
,
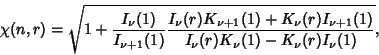 |
(4) |
where 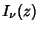 is a Modified Bessel Function of the First Kind and
is a Modified Bessel Function of the First Kind and 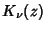 is a Modified Bessel Function
of the Second Kind. For
is a Modified Bessel Function
of the Second Kind. For 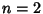 ,
,
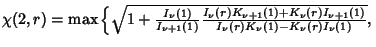
|
|
![$ \left.{\sqrt{1+{I_1(1)\over I_1(1)+I_2(1)}\left[{1+{I_1(r)K_0(1)+K_1(r)I_0(1)\over I_1(r)K_1(1)-K_1(r)I_1(1)}}\right]}}\right\}.\quad$](w_780.gif)
|
(5) |
For 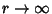 ,
,
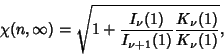 |
(6) |
which is bounded by
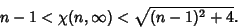 |
(7) |
For Odd 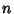 , the Recurrence Relations
, the Recurrence Relations
with
where e is the constant 2.71828..., give
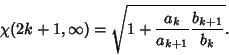 |
(14) |
The first few are
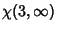 |
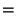 |
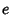 |
(15) |
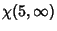 |
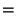 |
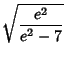 |
(16) |
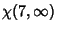 |
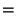 |
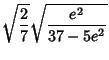 |
(17) |
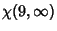 |
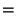 |
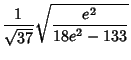 |
(18) |
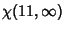 |
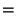 |
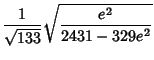 |
(19) |
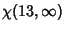 |
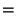 |
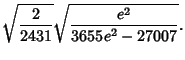 |
(20) |
Similar formulas can be given for even 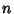 in terms of
in terms of 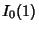 ,
, 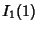 ,
, 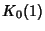 ,
, 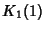 .
.
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/mkhln/mkhln.html
Mikhlin, S. G. Constants in Some Inequalities of Analysis. New York: Wiley, 1986.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be the
be the ![]() -D closed Ball of Radius
-D closed Ball of Radius ![]() centered at the Origin. A function which is
defined on
centered at the Origin. A function which is
defined on ![]() is called an extension to
is called an extension to ![]() of a function
of a function ![]() defined on
defined on ![]() if
if
![$\sqrt{\int_{B(1)} \left[{[f(x)]^2+\sum_{j=1}^n\left({\partial f\over\partial x_j}\right)^2}\right]\,dx} $](w_772.gif)
![$ \leq \chi \sqrt{\int_{B(r)} \left[{[F(x)]^2+\sum_{j=1}^n\left({\partial F\over\partial x_j}\right)^2}\right]\,dx}\,.\quad$](w_773.gif)
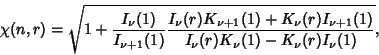
![$ \left.{\sqrt{1+{I_1(1)\over I_1(1)+I_2(1)}\left[{1+{I_1(r)K_0(1)+K_1(r)I_0(1)\over I_1(r)K_1(1)-K_1(r)I_1(1)}}\right]}}\right\}.\quad$](w_780.gif)