|
|
|
The Weingarten equations express the derivatives of the Normal using derivatives of the position vector. Let
![]() be a Regular Patch, then the Shape Operator
be a Regular Patch, then the Shape Operator ![]() of x is given in terms of the basis
of x is given in terms of the basis
![]() by
by
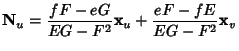 |
(1) | ||
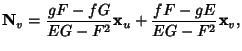 |
(2) |
| (3) |
| (4) | |||
| (5) | |||
| (6) |
See also Fundamental Forms, Shape Operator
References
Gray, A. ``Calculation of the Shape Operator.'' §14.3 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 274-277, 1993.