|
|
|
The constant also called the Parity Constant and defined by
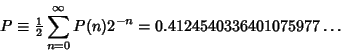 |
(1) |
The Thue-Morse constant can be written in base 2 by stages by taking the previous iteration ![]() , taking the complement
, taking the complement
![]() , and appending, producing
, and appending, producing
| (2) |
| (3) |
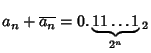 , which can be found from
, which can be found from
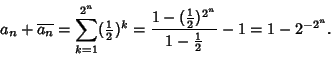 |
(4) |
| (5) |
| (6) |
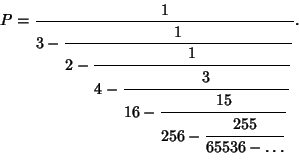 |
(7) |
| (8) |
The Sequence
![]() (Sloane's A010060) is known as the Thue-Morse Sequence.
(Sloane's A010060) is known as the Thue-Morse Sequence.
See also Rabbit Constant, Thue Constant
References
Allouche, J. P.; Arnold, A.; Berstel, J.; Brlek, S.; Jockusch, W.; Plouffe, S.; and Sagan, B.
``A Relative of the Thue-Morse Sequence.'' Discr. Math. 139, 455-461, 1995.
Allouche, J. P. and Shallit, J. In preparation.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT
Artificial Intelligence Laboratory, Memo AIM-239, Item 122, Feb. 1972.
Dekking, F. M. ``Transcendence du nombre de Thue-Morse.'' Comptes Rendus de l'Academie des Sciences de Paris 285, 157-160, 1977.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/cntfrc/cntfrc.html
Sloane, N. J. A. Sequences
A010060,
A014571, and
A014572
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein