|
|
|
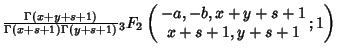
|
|
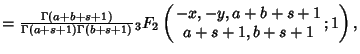
|
where ![]() is the Gamma Function and the function
is the Gamma Function and the function
![]() is a Generalized Hypergeometric Function.
is a Generalized Hypergeometric Function.
See also Generalized Hypergeometric Function
References
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed.
New York: Chelsea, pp. 104-105, 1959.