|
|
|
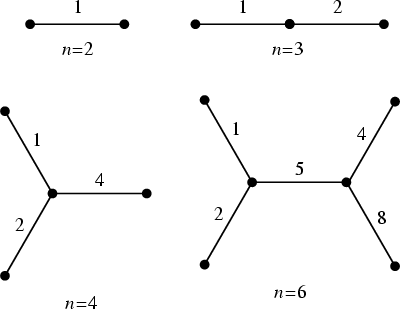
For a given Positive Integer ![]() , does there exist a Weighted Tree with
, does there exist a Weighted Tree with ![]() Vertices whose paths have weights 1, 2, ...,
Vertices whose paths have weights 1, 2, ..., ![]() , where
, where ![]() is a Binomial Coefficient?
Taylor showed that no such Tree can exist unless it is a Perfect Square or a Perfect Square plus 2.
No such Trees are known except
is a Binomial Coefficient?
Taylor showed that no such Tree can exist unless it is a Perfect Square or a Perfect Square plus 2.
No such Trees are known except ![]() , 3, 4, and 6.
, 3, 4, and 6.
See also Golomb Ruler, Perfect Difference Set
References
Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 56-60, 1985.
Leech, J. ``Another Tree Labeling Problem.'' Amer. Math. Monthly 82, 923-925, 1975.
Taylor, H. ``Odd Path Sums in an Edge-Labeled Tree.'' Math. Mag. 50, 258-259, 1977.