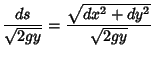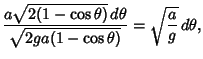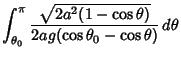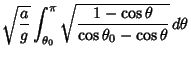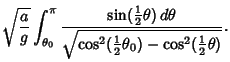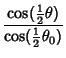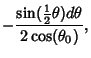Find the curve down which a bead placed anywhere will fall to the bottom in the same amount of time. The solution is a
Cycloid, a fact first discovered and published by Huygens  in Horologium oscillatorium (1673).
Huygens also constructed the first pendulum
in Horologium oscillatorium (1673).
Huygens also constructed the first pendulum  clock with a device to ensure that the
pendulum was isochronous by forcing the pendulum to swing in an arc of a Cycloid.
clock with a device to ensure that the
pendulum was isochronous by forcing the pendulum to swing in an arc of a Cycloid.
The parametric equations of the Cycloid are
To see that the Cycloid satisfies the tautochrone property, consider the derivatives
and
Now
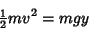 |
(6) |
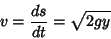 |
(7) |
so the time required to travel from the top of the Cycloid to the bottom is
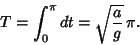 |
(9) |
However, from an intermediate point 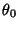 ,
,
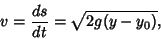 |
(10) |
so
Now let
so
![\begin{displaymath}
T=-2\sqrt{a\over g}\int_1^0 {du\over\sqrt{1-u^2}} = 2\sqrt{a\over g}\, [\sin^{-1}u]^1_0 = \pi\sqrt{a\over g}\,,
\end{displaymath}](t_232.gif) |
(14) |
and the amount of time is the same from any point!
See also Brachistochrone Problem, Cycloid
References
Muterspaugh, J.; Driver, T.; and Dick, J. E. ``The Cycloid and Tautochronism.''
http://php.indiana.edu/~jedick/project/intro.html.
Muterspaugh, J.; Driver, T.; and Dick, J. E. ``P221 Tautochrone Problem.''
http://php.indiana.edu/~jedick/project/project.html.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 54-60 and 384-385, 1991.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() in Horologium oscillatorium (1673).
Huygens also constructed the first pendulum
in Horologium oscillatorium (1673).
Huygens also constructed the first pendulum ![]() clock with a device to ensure that the
pendulum was isochronous by forcing the pendulum to swing in an arc of a Cycloid.
clock with a device to ensure that the
pendulum was isochronous by forcing the pendulum to swing in an arc of a Cycloid.