Let 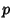 be a Prime Number,
be a Prime Number, 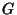 a Group, and
a Group, and 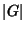 the order of
the order of 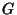 .
.
- 1. If
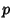 divides
divides 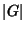 , then
, then 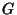 has a Sylow p-Subgroup.
has a Sylow p-Subgroup.
- 2. In a Finite Group, all the Sylow p-Subgroup are isomorphic for some
fixed
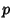 .
.
- 3. The number of Sylow p-Subgroup for a fixed
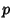 is Congruent to 1
(mod
is Congruent to 1
(mod 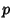 ).
).
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be a Prime Number,
be a Prime Number, ![]() a Group, and
a Group, and ![]() the order of
the order of ![]() .
.