Spider and Fly Problem

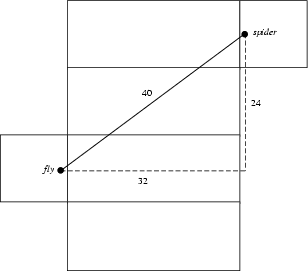
$\begin{figure}\begin{center}\BoxedEPSF{SpiderandFly.epsf scaled 500}\end{center}\end{figure}$

In a rectangular room (a Cuboid) with dimensions $30'\times 12'\times 12'$ , a spider is located in the middle of one $12'\times 12'$ wall one foot away from the ceiling. A fly is in the middle of the opposite wall one foot away from the floor. If the fly remains stationary, what is the shortest distance the spider must crawl to capture the fly? The answer, , can be obtained by ``flattening'' the walls as illustrated above.

References

Pappas, T. ``The Spider & the Fly Problem.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 218 and 233, 1989.