|
|
|
The generalization of a tetrahedral region of space to ![]() -D. The boundary of a
-D. The boundary of a ![]() -simplex has
-simplex has ![]() 0-faces
(Vertices),
0-faces
(Vertices), ![]() 1-faces (Edges), and
1-faces (Edges), and
![]()
![]() -faces, where
-faces, where ![]() is a Binomial Coefficient.
is a Binomial Coefficient.
The simplex in 4-D is a regular Tetrahedron ![]() in which a point
in which a point ![]() along the fourth dimension through
the center of
along the fourth dimension through
the center of ![]() is chosen so that
is chosen so that
![]() . The 4-D simplex has Schläfli Symbol
. The 4-D simplex has Schläfli Symbol ![]() .
.
| Simplex | |
| 0 | Point |
| 1 | Line Segment |
| 2 | Equilateral Triangular Plane Region |
| 3 | Tetrahedral Region |
| 4 | 4-simplex |
The regular simplex in ![]() -D with
-D with ![]() is denoted
is denoted ![]() and has Schläfli Symbol
and has Schläfli Symbol
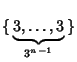 .
.
See also Complex, Cross Polytope, Equilateral Triangle, Line Segment, Measure Polytope, Nerve, Point, Simplex Method, Tetrahedron
References
Eppstein, D. ``Triangles and Simplices.''
http://www.ics.uci.edu/~eppstein/junkyard/triangulation.html.