Given a simple harmonic oscillator with a quadratic perturbation 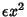 ,
,
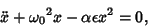 |
(1) |
find the first-order solution using a perturbation method. Write
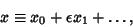 |
(2) |
so
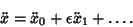 |
(3) |
Plugging (2) and (3) back into (1) gives
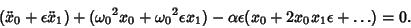 |
(4) |
Keeping only terms of order 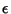 and lower and grouping, we obtain
and lower and grouping, we obtain
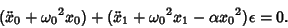 |
(5) |
Since this equation must hold for all Powers of 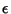 , we can separate it into the two differential equations
, we can separate it into the two differential equations
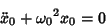 |
(6) |
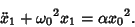 |
(7) |
The solution to (6) is just
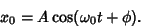 |
(8) |
Setting our clock so that 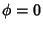 gives
gives
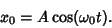 |
(9) |
Plugging this into (7) then gives
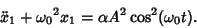 |
(10) |
The two homogeneous solutions to (10) are
The particular solution to (10) is therefore given by
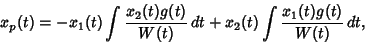 |
(13) |
where
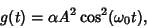 |
(14) |
and the Wronskian is
Plugging everything into (13),
Now let
Then
Plugging 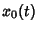 and (21) into (2), we obtain the solution
and (21) into (2), we obtain the solution
![\begin{displaymath}
x(t)=A\cos({\omega_0}t)-{\alpha A^2\over 6{\omega_0}^2}\epsilon [\cos(2{\omega_0}t)-3].
\end{displaymath}](s1_1344.gif) |
(22) |
© 1996-9 Eric W. Weisstein
1999-05-26
![]() ,
,
![$\displaystyle \alpha A^2\left[{-\cos({\omega_0}t)\int{\sin({\omega_0}t)\cos^2({...
...a_0}}\,dt+\sin({\omega_0}t)\int{\cos^3({\omega_0}t)\over{\omega_0}}\,dt}\right]$](s1_1327.gif)
![$\displaystyle {\alpha A^2\over {\omega_0}} \left\{{\sin({\omega_0}t)\int [1-\sin^2({\omega_0}t)]\cos({\omega_0}t)\, dt}\right.$](s1_1328.gif)
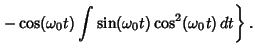
![$\displaystyle {\alpha A^2\over {\omega_0}^2} \left[{\sin({\omega_0}t)\int (1-u^2)\,du+\cos({\omega_0}t) \int v^2\,dv}\right]$](s1_1335.gif)
![$\displaystyle {\alpha A^2\over {\omega_0}^2} \left[{\sin({\omega_0}t)(1-{\textstyle{1\over 3}} u^3)+\cos({\omega_0}t) {\textstyle{1\over 3}} v^3}\right]$](s1_1336.gif)
![$\displaystyle {\alpha A^2\over {\omega_0}^2}\{\sin({\omega_0}t)[1-{\textstyle{1...
...in^3({\omega_0}t)]+{\textstyle{1\over 3}}\cos({\omega_0}t)\cos^3({\omega_0}t)\}$](s1_1337.gif)
![$\displaystyle {\alpha A^2\over {\omega_0}^2}\left\{{{\textstyle{1\over 3}}[\cos^4({\omega_0}t)- \sin^4({\omega_0}t)]+\sin^2({\omega_0}t)}\right\}$](s1_1338.gif)
![$\displaystyle {\alpha A^2\over {\omega_0}^2}\left\{{{\textstyle{1\over 3}}[\cos^2({\omega_0}t)-\sin^2({\omega_0}t)]+\sin^2({\omega_0}t)}\right\}$](s1_1339.gif)
![$\displaystyle {\alpha A^2\over {\omega_0}^2}{\textstyle{1\over 3}} [\cos^2({\omega_0}t)+2\sin^2({\omega_0}t)]$](s1_1340.gif)
![$\displaystyle {\alpha A^2\over 3{\omega_0}^2}[2-\cos^2({\omega_0}t)] = {\alpha A^2\over 3{\omega_0}^2} \{2-{\textstyle{1\over 2}}[1+\cos(2{\omega_0}t)]\}$](s1_1341.gif)
![$\displaystyle {\alpha A^2\over 6{\omega_0}^2}[3-\cos(2{\omega_0}t)].$](s1_1342.gif)