|
|
|
Define
![]() with
with ![]() Positive as
Positive as
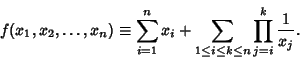
References
MacLeod, A. http://www.mathsoft.com/asolve/constant/shapiro/macleod.html.
Shallit, J. Solution by C. C. Grosjean and H. E. De Meyer. ``A Minimization Problem.''
Problem 94-15 in SIAM Review 37, 451-458, 1995.