A semiring is a set together with two Binary Operators 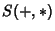 satisfying the following conditions:
satisfying the following conditions:
- 1. Additive associativity: For all
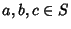 ,
,
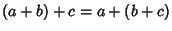 ,
,
- 2. Additive commutativity: For all
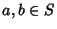 ,
, 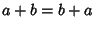 ,
,
- 3. Multiplicative associativity: For all
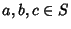 ,
,
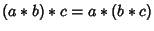 ,
,
- 4. Left and right distributivity: For all
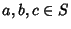 ,
,
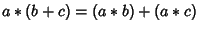 and
and
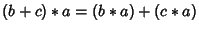 .
.
A semiring is therefore a commutative Semigroup under addition and a Semigroup under multiplication.
A semiring can be empty.
See also Binary Operator, Ring, Ringoid, Semigroup
References
Rosenfeld, A. An Introduction to Algebraic Structures. New York: Holden-Day, 1968.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() satisfying the following conditions:
satisfying the following conditions: