where 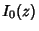 is a Modified Bessel Function of the First Kind and
is a Modified Bessel Function of the First Kind and
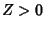 . For a derivation, see Papoulis (1962). For
. For a derivation, see Papoulis (1962). For 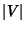 = 0, this reduces to the
Rayleigh Distribution.
= 0, this reduces to the
Rayleigh Distribution.
See also Rayleigh Distribution
References
Papoulis, A. The Fourier Integral and Its Applications. New York: McGraw-Hill, 1962.
© 1996-9 Eric W. Weisstein
1999-05-25