|
|
|
A generalization of Dilworth's Lemma. For each
![]() with
with ![]() , there exists a least
Integer
, there exists a least
Integer ![]() (the Ramsey Number) such that no matter how the Complete Graph
(the Ramsey Number) such that no matter how the Complete Graph ![]() is
two-colored, it will contain a green Subgraph
is
two-colored, it will contain a green Subgraph ![]() or a red Subgraph
or a red Subgraph ![]() . Furthermore,
. Furthermore,
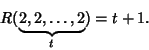
See also Dilworth's Lemma, Natural Independence Phenomenon, Pigeonhole Principle, Ramsey Number
References
Graham, R. L.; Rothschild, B. L.; and Spencer, J. H. Ramsey Theory, 2nd ed. New York: Wiley, 1990.
Spencer, J. ``Large Numbers and Unprovable Theorems.'' Amer. Math. Monthly 90, 669-675, 1983.