|
|
|
If
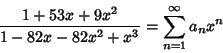 |
(1) |
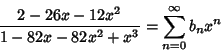 |
(2) |
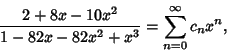 |
(3) |
| (4) |
| (5) | |||
| (6) | |||
| (7) |
| (8) | |||
| (9) |
References
Hirschhorn, M. D. ``An Amazing Identity of Ramanujan.'' Math. Mag. 68, 199-201, 1995.
Hirschhorn, M. D. ``A Proof in the Spirit of Zeilberger of an Amazing Identity of Ramanujan.'' Math. Mag. 69, 267-269, 1996.