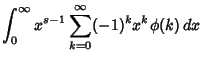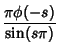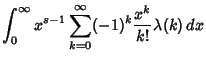where 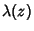 is the Dirichlet Lambda Function and
is the Dirichlet Lambda Function and 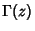 is the Gamma Function. Equation (2) is
obtained from (1) by defining
is the Gamma Function. Equation (2) is
obtained from (1) by defining
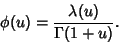 |
(3) |
These formulas give valid results only for certain classes of functions.
References
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 15
and 186-195, 1959.
© 1996-9 Eric W. Weisstein
1999-05-25