|
|
|
A generalization of simple majority voting in which a list of quotas
![]() specifies, according to the
number of votes, how many votes an alternative needs to win (Taylor 1995). The quota system declares a tie unless for some
specifies, according to the
number of votes, how many votes an alternative needs to win (Taylor 1995). The quota system declares a tie unless for some
![]() , there are exactly
, there are exactly ![]() tie votes in the profile and one of the alternatives has at least
tie votes in the profile and one of the alternatives has at least ![]() votes, in which case the
alternative is the choice.
votes, in which case the
alternative is the choice.
Let ![]() be the number of quota systems for
be the number of quota systems for ![]() voters and
voters and ![]() the number of quota systems for which
the number of quota systems for which ![]() , so
, so
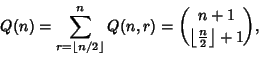
See also Binomial Coefficient, Central Binomial Coefficient
References
Sloane, N. J. A. Sequence
A001405/M0769
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Taylor, A. Mathematics and Politics: Strategy, Voting, Power, and Proof. New York: Springer-Verlag, 1995.
Young, S. C.; Taylor, A. D.; and Zwicker, W. S. ``Counting Quota Systems: A Combinatorial Question from Social Choice
Theory.'' Math. Mag. 68, 331-342, 1995.