|
|
|

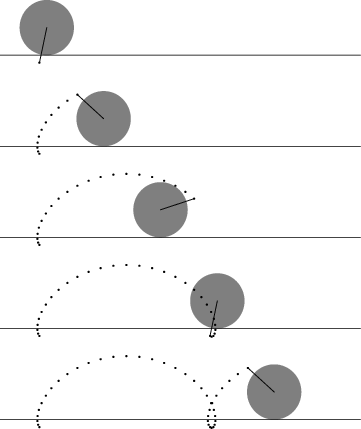
The path traced out by a fixed point at a Radius ![]() , where
, where ![]() is the Radius of a rolling Circle,
also sometimes called an Extended Cycloid. The prolate cycloid contains loops,
and has parametric equations
is the Radius of a rolling Circle,
also sometimes called an Extended Cycloid. The prolate cycloid contains loops,
and has parametric equations
| (1) | |||
| (2) |
| (3) |
| (4) |
| (5) |
See also Curtate Cycloid, Cycloid
References
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 46-50, 1991.