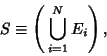Given an event 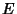 in a Sample Space
in a Sample Space 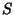 which is either finite with
which is either finite with 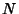 elements or countably infinite with
elements or countably infinite with
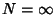 elements, then we can write
elements, then we can write
and a quantity 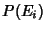 , called the Probability of event
, called the Probability of event 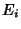 , is defined such that
, is defined such that
- 1.
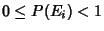 .
.
- 2.
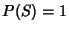 .
.
- 3. Additivity:
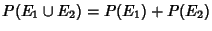 , where
, where 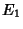 and
and 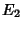 are mutually
exclusive.
are mutually
exclusive.
- 4. Countable additivity:
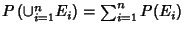 for
for
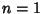 , 2, ...,
, 2, ..., 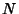 where
where 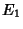 ,
, 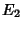 , ...are mutually exclusive (i.e.,
, ...are mutually exclusive (i.e.,
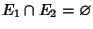 ).
).
See also Sample Space, Union
© 1996-9 Eric W. Weisstein
1999-05-26
![]() in a Sample Space
in a Sample Space ![]() which is either finite with
which is either finite with ![]() elements or countably infinite with
elements or countably infinite with
![]() elements, then we can write
elements, then we can write