Poker

Poker is a Card game played with a normal deck of 52 Cards. Sometimes, additional cards called ``jokers'' are also used. In straight or draw poker, each player is normally dealt a hand of five cards. Depending on the variant, players then discard and redraw Cards, trying to improve their hands. Bets are placed at each discard step. The number of possible distinct five-card hands is

$$N={52\choose 5} = 2{,}598{,}960,$$

where ${n\choose k}$ is a Binomial Coefficient.

There are special names for specific types of hands. A royal flush is an ace, king, queen, jack, and 10, all of one suit. A straight flush is five consecutive cards all of the same suit (but not a royal flush), where an ace may count as either high or low. A full house is three-of-a-kind and a pair. A flush is five cards of the same suit (but not a royal flush or straight flush). A straight is five consecutive cards (but not a royal flush or straight flush), where an ace may again count as either high or low.

The probabilities of being dealt five-card poker hands of a given type (before discarding and with no jokers) on the initial deal are given below (Packel 1981). As usual, for a hand with probability $P$, the Odds against being dealt it are $(1/r)-1:1$.

Hand	Exact Probability	Probability	Odds
royal flush	${4\over N} = {1\over 649{,}740}$	$1.54\times 10^{-6}$	649,739.0:1
straight flush	${4(10)-4\over N} = {3\over 216{,}580}$	$1.39\times 10^{-5}$	72,192.3:1
four of a kind	${13(48)\over N} = {1\over 4{,}165}$	$2.40\times 10^{-4}$	4,164.0:1
full house	${13{4\choose 3}12{4\choose 2}\over N} = {6\over 4{,}165}$	$1.44\times 10^{-3}$	693.2:1
flush	${4{13\choose 5}-36-4\over N} = {1{,}277\over 649{,}740}$	$1.97\times 10^{-3}$	507.8:1
straight	${10(4^5)-36-4\over N} = {5\over 1{,}274}$	$3.92\times 10^{-3}$	253.8:1
three of a kind	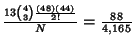${13{4\choose 3}{(48)(44)\over 2!}\over N} = {88\over 4{,}165}$	0.0211	46.3:1
two pair	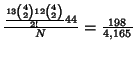${{13{4\choose 2}12{4\choose 2}\over 2!}44\over N} = {198\over 4{,}165}$	0.0475	20.0:1
one pair	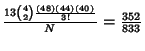${13{4\choose 2}{(48)(44)(40)\over 3!}\over N} = {352\over 833}$	0.423	1.366:1

Gadbois (1996) gives probabilities for hands if two jokers are included, and points out that it is impossible to rank hands in any single way which is consistent with the relative frequency of the hands.

See also Bridge Card Game, Cards

References

Cheung, Y. L. ``Why Poker is Played with Five Cards.'' Math. Gaz. 73, 313-315, 1989.

Conway, J. H. and Guy, R. K. ``Choice Numbers with Repetitions.'' In The Book of Numbers. New York: Springer-Verlag, pp. 70-71, 1996.

Gadbois, S. ``Poker with Wild Cards--A Paradox?'' Math. Mag. 69, 283-285, 1996.

Jacoby, O. Oswald Jacoby on Poker. New York: Doubleday, 1981.

Packel, E. W. The Mathematics of Games and Gambling. Washington, DC: Math. Assoc. Amer., 1981.