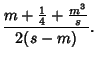A number 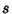 Trials in which the probability of success
Trials in which the probability of success 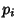 varies from trial to trial. Let
varies from trial to trial. Let 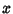 be
the number of successes, then
be
the number of successes, then
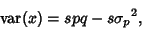 |
(1) |
where 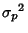 is the Variance of
is the Variance of 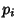 and
and 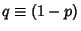 . Uspensky has shown that
. Uspensky has shown that
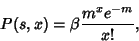 |
(2) |
where
and
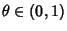 . The probability that the number of successes is at least
. The probability that the number of successes is at least 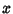 is given by
is given by
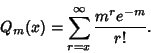 |
(6) |
Uspensky gives the true probability that there are at least 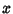 successes in
successes in 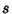 trials as
trials as
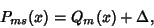 |
(7) |
where
© 1996-9 Eric W. Weisstein
1999-05-25
![]() Trials in which the probability of success
Trials in which the probability of success ![]() varies from trial to trial. Let
varies from trial to trial. Let ![]() be
the number of successes, then
be
the number of successes, then
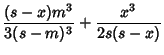
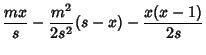
![$\displaystyle p\left[{{x\over 2}\left({1+{1\over m}}\right)-{(x-m)^2\over 2m}}\right]$](p2_1063.gif)
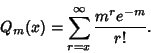
![$\displaystyle \left\{\begin{array}{ll} (e^\chi-1)Q_m(x+1) & \mbox{for $Q_m(x+1)...
...-Q_m(x+1)] & \mbox{for $Q_m(x+1)\leq {\textstyle{1\over 2}}$}\end{array}\right.$](p2_1068.gif)