|
|
|
Let ![]() and
and ![]() be infinitely differentiable functions of
be infinitely differentiable functions of ![]() and
and ![]() . Then the Poisson bracket is defined by
. Then the Poisson bracket is defined by
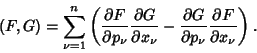
See also Lagrange Bracket, Lie Bracket
References
Iyanaga, S. and Kawada, Y. (Eds.). Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1004, 1980.