|
|
|
Let ![]() be a set of orthonormal vectors with
be a set of orthonormal vectors with ![]() , 2, ...,
, 2, ..., ![]() , such that the Inner Product
, such that the Inner Product
![]() . Then set
. Then set
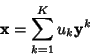 |
(1) |
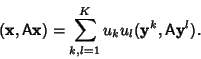 |
(2) |
| (3) |
| (4) |
| (5) |
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1120, 1979.