|
|
|
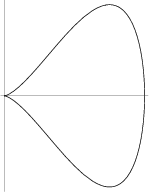
A plane curve also called the Peg Top and given by the Cartesian equation
| (1) |
| (2) | |||
| (3) |
| (4) |

See also Butterfly Curve, Dumbbell Curve, Eight Curve, Heart Surface, Pear Curve
References
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub. p. 71, 1989.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 148-150, 1972.
Nordstrand, T. ``Surfaces.''
http://www.uib.no/people/nfytn/surfaces.htm.