|
|
|
An Operator which describes the time evolution of densities in Phase Space. The Operator can be defined
by
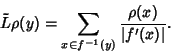
References
Beck, C. and Schlögl, F. ``Transfer Operator Methods.'' Ch. 17 in Thermodynamics of Chaotic Systems.
Cambridge, England: Cambridge University Press, pp. 190-203, 1995.