Peaucellier Inversor

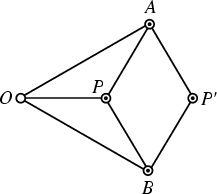
A Linkage with six rods which draws the inverse of a given curve. When a pencil is placed at $P$, the inverse is drawn at $P'$ (or vice versa). If a seventh rod (dashed) is added (with an additional pivot), $P$ is kept on a circle and the locus traced out by $P'$ is a straight line. It therefore converts circular motion to linear motion without sliding, and was discovered in 1864. Another Linkage which performs this feat using hinged squares had been published by Sarrus in 1853 but ignored. Coxeter (1969, p. 428) shows that

$$OP\times OP'=OA^2-PA^2.$$

See also Hart's Inversor, Linkage

References

Bogomolny, A. ``Peaucellier Linkage.'' http://www.cut-the-knot.com/pythagoras/invert.html.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods. Oxford, England: Oxford University Press, p. 156, 1978.

Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 82-83, 1969.

Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 46-48, 1990.

Rademacher, H. and Toeplitz, O. The Enjoyment of Mathematics: Selections from Mathematics for the Amateur. Princeton, NJ: Princeton University Press, pp. 121-126, 1957.

Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 324, 1994.