Proved in 1933. If 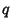 is an Odd Prime or
is an Odd Prime or 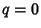 and
and 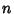 is any Positive Integer, then there is a
Hadamard Matrix of order
is any Positive Integer, then there is a
Hadamard Matrix of order
where 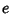 is any Positive Integer such that
is any Positive Integer such that
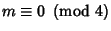 . If
. If 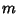 is of this form, the matrix can be constructed
with a Paley Construction. If
is of this form, the matrix can be constructed
with a Paley Construction. If 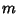 is divisible by 4 but not of the form (1), the Paley Class is undefined.
However, Hadamard Matrices have been shown to exist for all
is divisible by 4 but not of the form (1), the Paley Class is undefined.
However, Hadamard Matrices have been shown to exist for all
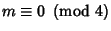 for
for 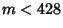 .
.
See also Hadamard Matrix, Paley Class, Paley Construction
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is an Odd Prime or
is an Odd Prime or ![]() and
and ![]() is any Positive Integer, then there is a
Hadamard Matrix of order
is any Positive Integer, then there is a
Hadamard Matrix of order