|
|
|
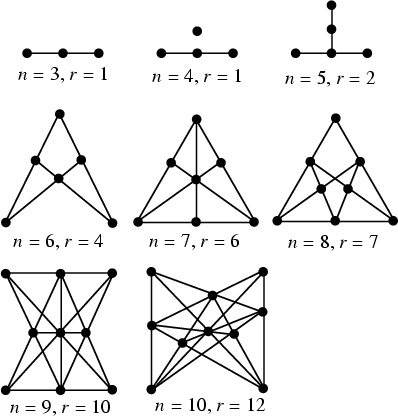
Also known as the Tree-Planting Problem. Plant ![]() trees so that there will be
trees so that there will be ![]() straight rows with
straight rows with ![]() trees
in each row. The following table gives max(
trees
in each row. The following table gives max(![]() ) for various
) for various ![]() .
. ![]() is Sloane's A003035 and
is Sloane's A003035 and ![]() is Sloane's A006065.
is Sloane's A006065.
| 3 | 1 | -- | -- |
| 4 | 1 | 1 | -- |
| 5 | 2 | 1 | 1 |
| 6 | 4 | 1 | 1 |
| 7 | 6 | 2 | 1 |
| 8 | 7 | 2 | 1 |
| 9 | 10 | 3 | 2 |
| 10 | 12 | 5 | 2 |
| 11 | 16 | 6 | 2 |
| 12 | 19 | 7 | 3 |
| 13 | 3 | ||
| 14 | 4 | ||
| 15 | |||
| 16 | 37 | ||
| 17 | |||
| 18 | |||
| 19 | |||
| 20 | |||
| 21 | |||
| 22 | |||
| 23 | |||
| 24 | |||
| 25 |
Sylvester showed that
See also Orchard Visibility Problem
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York:
Dover, pp. 104-105 and 129, 1987.
Burr, S. A. ``Planting Trees.'' In The Mathematical Gardner (Ed. David Klarner). Boston, MA: Prindle, Weber,
and Schmidt, pp. 90-99, 1981.
Dudeney, H. E. Problem 435 in 536 Puzzles & Curious Problems. New York: Scribner, 1967.
Dudeney, H. E. The Canterbury Puzzles and Other Curious Problems, 7th ed.
London: Thomas Nelson and Sons, p. 175, 1949.
Dudeney, H. E. §213 in Amusements in Mathematics. New York: Dover, 1970.
Gardner, M. Ch. 2 in Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American.
New York: Vintage Books, 1977.
Gardner, M. ``Tree-Plant Problems.'' Ch. 22 in Time Travel and Other Mathematical Bewilderments.
New York: W. H. Freeman, pp. 277-290, 1988.
Grünbaum, B. ``New Views on Some Old Questions of Combinatorial Geometry.'' Teorie Combin. 1, 451-468, 1976.
Grünbaum, B. and Sloane, N. J. A. ``The Orchard Problem.'' Geom. Dedic. 2, 397-424, 1974.
Jackson, J. Rational Amusements for Winter Evenings. London, 1821.
Macmillan, R. H. ``An Old Problem.'' Math. Gaz. 30, 109, 1946.
Sloane, N. J. A. Sequences
A006065/M0290
and A003035/M0982
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein