|
|
|
If there is only one Critical Point, it must be the Extremum for functions of one variable. There are
exceptions for two variables, but none of degree ![]() . Such exceptions include
. Such exceptions include
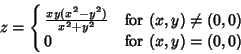
References
Ash, A. M. and Sexton, H. ``A Surface with One Local Minimum.'' Math. Mag. 58, 147-149, 1985.
Calvert, B. and Vamanamurthy, M. K. ``Local and Global Extrema for Functions of Several Variables.''
J. Austral. Math. Soc. 29, 362-368, 1980.
Davies, R. Solution to Problem 1235. Math. Mag. 61, 59, 1988.
Wagon, S. ``Failure of the Only-Critical-Point-in-Town Test.'' §3.4 in Mathematica in Action.
New York: W. H. Freeman, pp. 87-91 and 228, 1991.