|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
An infinite sequence of Positive Integers
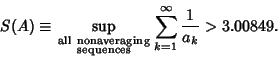
References
Behrend, F. ``On Sets of Integers which Contain no Three Terms in an Arithmetic Progression.''
Proc. Nat. Acad. Sci. USA 32, 331-332, 1946.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/erdos/erdos.html
Gerver, J. L. ``The Sum of the Reciprocals of a Set of Integers with No Arithmetic Progression of
Gerver, J. L. and Ramsey, L. ``Sets of Integers with no Long Arithmetic Progressions Generated by the Greedy
Algorithm.'' Math. Comput. 33, 1353-1360, 1979.
Guy, R. K. ``Nonaveraging Sets. Nondividing Sets.'' §C16 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 131-132, 1994.
Wróblewski, J. ``A Nonaveraging Set of Integers with a Large Sum of Reciprocals.'' Math. Comput. 43, 261-262, 1984.
![]() Terms.''
Proc. Amer. Math. Soc. 62, 211-214, 1977.
Terms.''
Proc. Amer. Math. Soc. 62, 211-214, 1977.