Nonassociative Algebra

An Algebra which does not satisfy

$$a(bc)=(ab)c$$

is called a nonassociative algebra. Bott and Milnor (1958) proved that the only Division Algebras are for 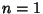$n = 1$, 2, 4, and 8. Each gives rise to an Algebra with particularly useful physical applications (which, however, is not itself necessarily nonassociative), and these four cases correspond to Real Numbers, Complex Numbers, Quaternions, and Cayley Numbers, respectively.

See also Algebra, Cayley Number, Complex Number, Division Algebra, Quaternion, Real Number

References

Bott, R. and Milnor, J. ``On the Parallelizability of the Spheres.'' Bull. Amer. Math. Soc. 64, 87-89, 1958.