Let 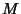 be a finitely generated Module over a commutative Noetherian Ring
be a finitely generated Module over a commutative Noetherian Ring 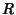 . Then there exists a
finite set
. Then there exists a
finite set
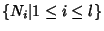 of submodules of
of submodules of 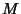 such that
such that
- 1.
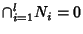 and
and
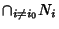 is not contained in
is not contained in 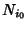 for all
for all
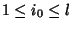 .
.
- 2. Each quotient
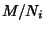 is primary for some prime
is primary for some prime 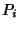 .
.
- 3. The
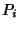 are all distinct for
are all distinct for 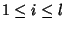 .
.
- 4. Uniqueness of the primary component
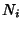 is equivalent to the statement that
is equivalent to the statement that 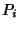 does not contain
does not contain 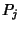 for any
for any
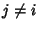 .
.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be a finitely generated Module over a commutative Noetherian Ring
be a finitely generated Module over a commutative Noetherian Ring ![]() . Then there exists a
finite set
. Then there exists a
finite set
![]() of submodules of
of submodules of ![]() such that
such that