|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Given a Positive Integer ![]() , let its Prime Factorization be written
, let its Prime Factorization be written
| (1) |
| (2) | |||
| (3) |
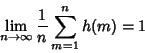 |
(4) |
| (5) |
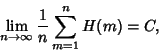 |
(6) |
![\begin{displaymath}
C=1+\left\{{\sum_{j=2}^\infty \left[{1-{1\over\zeta(j)}}\right]}\right\}=1.705221\ldots
\end{displaymath}](n_644.gif) |
(7) |
The Continued Fraction of Niven's constant is 1, 1, 2, 2, 1, 1, 4, 1, 1, 3, 4, 4, 8, 4, 1, ... (Sloane's A033151). The positions at which the digits 1, 2, ... first occur in the Continued Fraction are 1, 3, 10, 7, 47, 41, 34, 13, 140, 252, 20, ... (Sloane's A033152). The sequence of largest terms in the Continued Fraction is 1, 2, 4, 8, 11, 14, 29, 372, 559, ... (Sloane's A033153), which occur at positions 1, 3, 7, 13, 20, 35, 51, 68, 96, ... (Sloane's A033154).
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/niven/niven.html
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 41, 1983.
Niven, I. ``Averages of Exponents in Factoring Integers.'' Proc. Amer. Math. Soc. 22, 356-360, 1969.
Plouffe, S. ``The Niven Constant.'' http://www.lacim.uqam.ca/piDATA/niven.txt.
Sloane, N. J. A. Sequences
A033150,
A033151,
A033152,
A033153, and
A033154
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein