|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
N. Nielsen (1909) and Ramanujan (Berndt 1985) considered the integrals
| (1) |
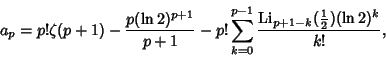 |
(2) |
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
See also Polylogarithm, Riemann Zeta Function
References
Berndt, B. C. Ramanujan's Notebooks, Part I. New York: Springer-Verlag, 1985.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/nielram/nielram.html
Flajolet, P. and Salvy, B. ``Euler Sums and Contour Integral Representation.'' Submitted to Experim. Math 1997.
http://pauillac.inria.fr/algo/flajolet/Publications/publist.html.