|
|
|
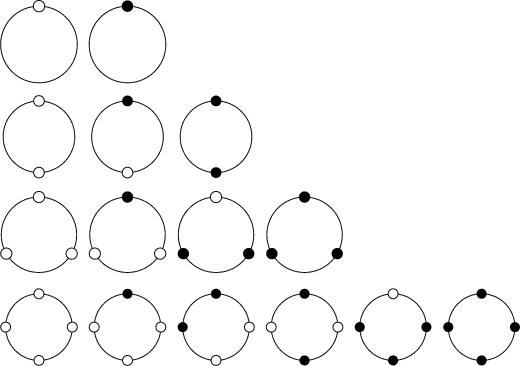
In the technical Combinatorial sense, an ![]() -ary necklace
-ary necklace ![]() of length
of length ![]() is a string of
is a string of ![]() characters, each of
characters, each of ![]() possible types. Rotation is ignored, in the sense that
possible types. Rotation is ignored, in the sense that
![]() is equivalent to
is equivalent to
![]() for any
for any ![]() , but reversal of strings is respected. Necklaces therefore correspond to
circular collections of beads in which the Fixed necklace may not be picked up out of the Plane (so that opposite
orientations are not considered equivalent).
, but reversal of strings is respected. Necklaces therefore correspond to
circular collections of beads in which the Fixed necklace may not be picked up out of the Plane (so that opposite
orientations are not considered equivalent).
The number of distinct Free necklaces ![]() of
of ![]() beads, each of
beads, each of ![]() possible colors, in which opposite orientations
(Mirror Images) are regarded as equivalent (so the necklace can be picked up out of the
Plane and flipped over) can be found as follows. Find the Divisors of
possible colors, in which opposite orientations
(Mirror Images) are regarded as equivalent (so the necklace can be picked up out of the
Plane and flipped over) can be found as follows. Find the Divisors of ![]() and label them
and label them ![]() ,
, ![]() , ...,
, ...,
![]() where
where ![]() is the number of Divisors of
is the number of Divisors of ![]() . Then
. Then
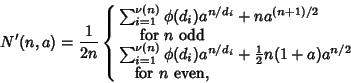
A table of the first few numbers of necklaces for ![]() and
and ![]() follows. Note that
follows. Note that ![]() is larger than
is larger than ![]() for
for
![]() . For
. For ![]() , the necklace 110100 is inequivalent to its Mirror Image 0110100, accounting for the difference
of 1 between
, the necklace 110100 is inequivalent to its Mirror Image 0110100, accounting for the difference
of 1 between ![]() and
and ![]() . Similarly, the two necklaces 0010110 and 0101110 are inequivalent to their reversals,
accounting for the difference of 2 between
. Similarly, the two necklaces 0010110 and 0101110 are inequivalent to their reversals,
accounting for the difference of 2 between ![]() and
and ![]() .
.
| Sloane | Sloane's A000031 | Sloane's A000029 | Sloane's A027671 |
| 1 | 2 | 2 | 3 |
| 2 | 3 | 3 | 6 |
| 3 | 4 | 4 | 10 |
| 4 | 6 | 6 | 21 |
| 5 | 8 | 8 | 39 |
| 6 | 14 | 13 | 92 |
| 7 | 20 | 18 | 198 |
| 8 | 36 | 30 | 498 |
| 9 | 60 | 46 | 1219 |
| 10 | 108 | 78 | 3210 |
| 11 | 188 | 126 | 8418 |
| 12 | 352 | 224 | 22913 |
| 13 | 632 | 380 | 62415 |
| 14 | 1182 | 687 | 173088 |
| 15 | 2192 | 1224 | 481598 |
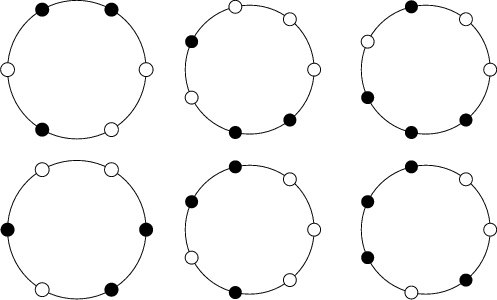
Ball and Coxeter (1987) consider the problem of finding the number of distinct arrangements of ![]() people in a ring such that
no person has the same two neighbors two or more times. For 8 people, there are 21 such arrangements.
people in a ring such that
no person has the same two neighbors two or more times. For 8 people, there are 21 such arrangements.
See also Antoine's Necklace, de Bruijn Sequence, Fixed, Free, Irreducible Polynomial, Josephus Problem, Lyndon Word
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 49-50, 1987.
Dudeney, H. E. Problem 275 in 536 Puzzles & Curious Problems. New York: Scribner, 1967.
Gardner, M. Martin Gardner's New Mathematical Diversions from Scientific American. New York: Simon and Schuster,
pp. 240-246, 1966.
Gilbert, E. N. and Riordan, J. ``Symmetry Types of Periodic Sequences.'' Illinois J. Math. 5, 657-665, 1961.
Riordan, J. ``The Combinatorial Significance of a Theorem of Pólya.'' J. SIAM 4, 232-234, 1957.
Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, p. 162, 1980.
Ruskey, F. ``Information on Necklaces, Lyndon Words, de Bruijn Sequences.''
http://sue.csc.uvic.ca/~cos/inf/neck/NecklaceInfo.html.
Sloane, N. J. A. Sequences A000029/M0563, A000031/M0564, A001869/M3860, and A027671 in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein