|
|
|
A Surface which a monkey can straddle with both his two legs and his tail. A simply Cartesian equation for such a
surface is
| (1) |
| (2) | |||
| (3) | |||
| (4) |
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) |
| (11) |
| (12) |
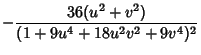 |
(13) | ||
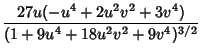 |
(14) |
See also Crossed Trough, Partial Derivative
References
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, p. 365, 1969.
Gray, A. Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 213-215, 262-263, and 288-289, 1993.
Hilbert, D. and Cohn-Vossen, S. Geometry and the Imagination. New York: Chelsea, p. 202, 1952.
|
|
|
© 1996-9 Eric W. Weisstein