|
|
|
Let
![]() be an infinite set of disjoint open Disks
be an infinite set of disjoint open Disks ![]() of radius
of radius ![]() such that the union is
almost the unit Disk. Then
such that the union is
almost the unit Disk. Then
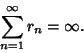 |
(1) |
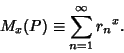 |
(2) |
| (3) |
| (4) |
References
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, pp. 36-37, 1983.
Mandelbrot, B. B. Fractals. San Francisco, CA: W. H. Freeman, p. 187, 1977.
Melzack, Z. A. ``On the Solid Packing Constant for Circles.'' Math. Comput. 23, 1969.