|
|
|
The first Simple Sporadic Groups discovered. ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() were discovered in 1861 and 1873 by Mathieu. Frobenius showed that all the Mathieu groups are
Subgroups of
were discovered in 1861 and 1873 by Mathieu. Frobenius showed that all the Mathieu groups are
Subgroups of ![]() .
.
The Mathieu groups are most simply defined as Automorphism groups of Steiner Systems.
![]() corresponds to
corresponds to ![]() and
and ![]() corresponds to
corresponds to ![]() .
. ![]() and
and ![]() are Transitive
Permutation Groups of 11 and 23 elements.
are Transitive
Permutation Groups of 11 and 23 elements.
The Orders of the Mathieu groups are
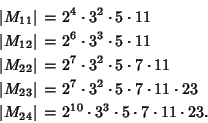
See also Sporadic Group
References
Conway, J. H. and Sloane, N. J. A. ``The Golay Codes and the Mathieu Groups.''
Ch. 11 in Sphere Packings, Lattices, and Groups, 2nd ed.
New York: Springer-Verlag, pp. 299-330, 1993.
Rotman, J. J. Ch. 9 in An Introduction to the Theory of Groups, 4th ed. New York: Springer-Verlag, 1995.
Wilson, R. A. ``ATLAS of Finite Group Representation.''
http://for.mat.bham.ac.uk/atlas/html/contents.html#spo.