|
|
|
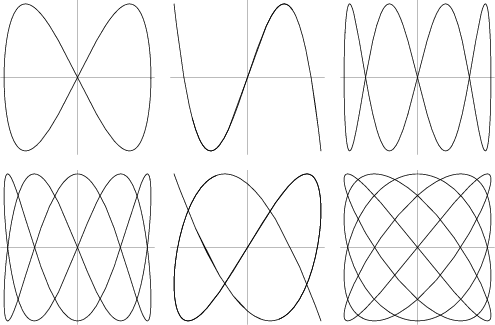
Lissajous curves are the family of curves described by the parametric equations
| (1) | |||
| (2) |
| (3) | |||
| (4) |
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press,
pp. 53-54, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 178-179 and 181-183, 1972.
MacTutor History of Mathematics Archive. ``Lissajous Curves.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Lissajous.html.