A linear congruence
is solvable Iff the Congruence
is solvable, where 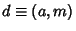 is the Greatest Common Divisor, in which case the solutions are
is the Greatest Common Divisor, in which case the solutions are 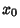 ,
, 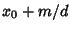 ,
,
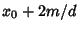 , ...,
, ..., 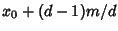 , where
, where 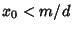 . If
. If 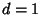 , then there is only one solution.
, then there is only one solution.
See also Congruence, Quadratic Congruence
© 1996-9 Eric W. Weisstein
1999-05-25