|
|
|
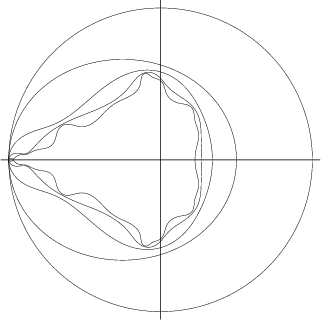
A curve on which points of a Map ![]() (such as the Mandelbrot Set) diverge to a given value
(such as the Mandelbrot Set) diverge to a given value ![]() at
the same rate. A common method of obtaining lemniscates is to define an Integer called the Count which is the
largest
at
the same rate. A common method of obtaining lemniscates is to define an Integer called the Count which is the
largest ![]() such that
such that ![]() where
where ![]() is usually taken as
is usually taken as ![]() . Successive Counts then define a series of
lemniscates, which are called Equipotential Curves by Peitgen and Saupe (1988).
. Successive Counts then define a series of
lemniscates, which are called Equipotential Curves by Peitgen and Saupe (1988).
See also Count, Mandelbrot Set
References
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images.
New York: Springer-Verlag, pp. 178-179, 1988.