|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Define the ![]() th Lebesgue constant for the Lagrange Interpolating Polynomial by
th Lebesgue constant for the Lagrange Interpolating Polynomial by
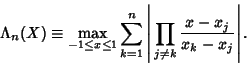 |
(1) |
| (2) |
| (3) |
| (4) |
References
Erdös, P. ``Problems and Results on the Theory of Interpolation, II.'' Acta Math. Acad. Sci. Hungary 12, 235-244, 1961.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lbsg/lbsg.html