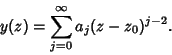A procedure for determining the behavior of an 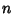 th order Ordinary Differential Equation at a Removable
Singularity without actually solving the equation. Consider
th order Ordinary Differential Equation at a Removable
Singularity without actually solving the equation. Consider
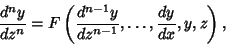 |
(1) |
where 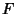 is Analytic in
is Analytic in 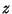 and rational in its other arguments. Proceed by making the
substitution
and rational in its other arguments. Proceed by making the
substitution
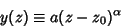 |
(2) |
with 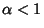 . For example, in the equation
. For example, in the equation
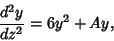 |
(3) |
making the substitution gives
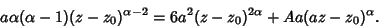 |
(4) |
The most singular terms (those with the most Negative exponents) are called the ``dominant balance terms,'' and must
balance exponents and Coefficients at the Singularity. Here, the first two terms are dominant, so
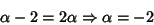 |
(5) |
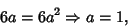 |
(6) |
and the solution behaves as
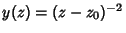 . The behavior in the Neighborhood of the Singularity is
given by expansion in a Laurent Series, in this case,
. The behavior in the Neighborhood of the Singularity is
given by expansion in a Laurent Series, in this case,
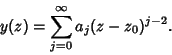 |
(7) |
Plugging this series in yields
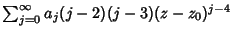
|
|
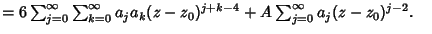
|
(8) |
This gives Recurrence Relations, in this case with 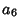 arbitrary, so the
arbitrary, so the 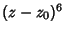 term is called the resonance or Kovalevskaya Exponent. At the resonances, the Coefficient will always be
arbitrary. If no resonance term is present, the Pole present is not ordinary, and the solution must be
investigated using a Psi Function.
term is called the resonance or Kovalevskaya Exponent. At the resonances, the Coefficient will always be
arbitrary. If no resonance term is present, the Pole present is not ordinary, and the solution must be
investigated using a Psi Function.
See also Psi Function
References
Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley,
p. 330, 1989.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() th order Ordinary Differential Equation at a Removable
Singularity without actually solving the equation. Consider
th order Ordinary Differential Equation at a Removable
Singularity without actually solving the equation. Consider