|
|
|
A special case of Enneper's Negative Curvature Surfaces which can be given parametrically by
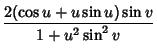 |
(1) | ||
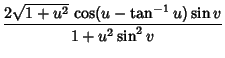 |
(2) | ||
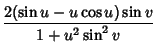 |
(3) | ||
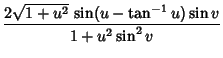 |
(4) | ||
| (5) |
![$\displaystyle -{u\cos({\textstyle{1\over 2}}v)[-2-u^2+u^2\cos(2v)]^4\sin({\textstyle{1\over 2}}v)\over 2[2-u^2+u^2\cos(2v)](1+u^2\sin^2 v)^4}$](k_879.gif) |
(6) | ||
![$\displaystyle {[-2-u^2+u^2\cos(2v)]^4[2-u^2+u^2\cos(2v)]\csc(v)\over 64u(1+u^2\sin^2 v)^4}.$](k_880.gif) |
|||
| (7) |
See also Enneper's Negative Curvature Surfaces, Rembs' Surfaces, Sievert's Surface
References
Fischer, G. (Ed.). Plate 86 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, p. 82, 1986.
Gray, A. ``Kuen's Surface.'' §19.4 in Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 384-386, 1993.
Kuen, T. ``Ueber Flächen von constantem Krümmungsmaass.'' Sitzungsber. d. königl. Bayer. Akad. Wiss. Math.-phys. Classe,
Heft II, 193-206, 1884.
Nordstrand, T. ``Kuen's Surface.''
http://www.uib.no/people/nfytn/kuentxt.htm.
Reckziegel, H. ``Kuen's Surface.'' §3.4.4.2 in
Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer).
Braunschweig, Germany: Vieweg, p. 38, 1986.