|
|
|
Jordan's lemma shows the value of the Integral
| (1) |
| (2) |
To derive the lemma, write
| (3) | |||
| (4) |
| (5) |
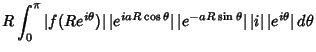 |
|||
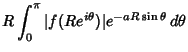 |
|||
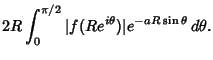 |
(6) |
| (7) |
| (8) |
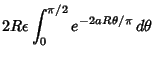 |
|||
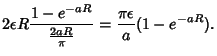 |
(9) |
| (10) |
See also Contour Integration
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 406-408, 1985.
|
|
|
© 1996-9 Eric W. Weisstein